CLASSICAL ENCRYPTION TECHNIQUES
There are two basic building blocks of all encryption techniques: substitution and transposition.
1 SUBSTITUTION TECHNIQUES
A substitution technique is one in which the letters of plaintext are replaced by other letters or by numbers or symbols. If the plaintext is viewed as a sequence of bits, then substitution involves replacing plaintext bit patterns with cipher text bit patterns.
(i)Caesar cipher (or) shift cipher
The earliest known use of a substitution cipher and the simplest was by Julius Caesar. The Caesar cipher involves replacing each letter of the alphabet with the letter standing 3 places further down the alphabet.
e.g., Plain text : pay more mone Cipher text: SDB PRUH PRQHB
Note that the alphabet is wrapped around, so that letter following „z‟ is „a‟. For each plaintext letter p, substitute the cipher text letter c such that C =
E(p) = (p+3) mod 26
A shift may be any amount, so that general Caesar algorithm is C = E (p) = (p+k) mod 26
Where k takes on a value in the range 1 to 25. The decryption algorithm is simply P = D(C) = (C-k) mod 26
(ii)Playfair cipher
The best known multiple letter encryption cipher is the playfair, which treats digrams in the plaintext as single units and translates these units into cipher text digrams. The playfair algorithm is based on the use of 5x5 matrix of letters constructed using a keyword. Let the keyword be „monarchy‟. The matrix is constructed by filling in the letters of the keyword (minus duplicates) from left to right and from top to bottom, and then filling in the remainder of the matrix with the remaining letters in alphabetical order.
The letter „i‟ and „j‟ count as one letter. Plaintext is encrypted two letters at a time according to the following rules:
Repeating plaintext letters that would fall in the same pair are separated with a filler letter such as „x‟.
Plaintext letters that fall in the same row of the matrix are each replaced by the letter to the right, with the first element of the row following the last.
Plaintext letters that fall in the same column are replaced by the letter beneath, with the top element of the column following the last.
Otherwise, each plaintext letter is replaced by the letter that lies in its own row and the column occupied by the other plaintext letter.
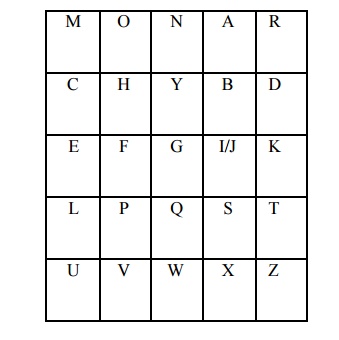
Plaintext = meet me at the school house
Splitting two letters as a unit => me et me at th es ch ox ol ho us ex Corresponding cipher text => CL KL CL RS PD IL HY AV MP HF XL IU
Strength of playfair cipher
Playfair cipher is a great advance over simple mono alphabetic ciphers.
Since there are 26 letters, 26x26 = 676 diagrams are possible, so identification of individual digram is more difficult.
Frequency analysis is much more difficult.
(iii)Polyalphabetic ciphers
Another way to improve on the simple monoalphabetic technique is to use different monoalphabetic substitutions as one proceeds through the plaintext message. The general name for this approach is polyalphabetic cipher. All the techniques have the following features in common.
A set of related monoalphabetic substitution rules are used
A key determines which particular rule is chosen for a given transformation.
(iv)Vigenere cipher
In this scheme, the set of related monoalphabetic substitution rules consisting of 26 caesar ciphers with shifts of 0 through 25. Each cipher is denoted by a key letter. e.g.,
Caesar cipher with a shift of 3 is denoted by the key value 'd‟ (since a=0, b=1, c=2 and so on). To aid in understanding the scheme, a matrix known as vigenere tableau is constructed.
Each of the 26 ciphers is laid out horizontally, with the key letter for each cipher to its left. A normal alphabet for the plaintext runs across the top. The process of encryption is simple: Given a key letter X and a plaintext letter y, the cipher text is at the intersection of the row labeled x and the column labeled y; in this case, the ciphertext is V.
To encrypt a message, a key is needed that is as long as the message. Usually, the key is a repeating keyword.
e.g., key = d e c e p t i v e d e c e p t i v e d e c e p t i v e
PT = w e a r e d i s c o v e r e d s a v e y o u r s e l f
CT = ZICVTWQNGRZGVTWAVZHCQYGLMGJ
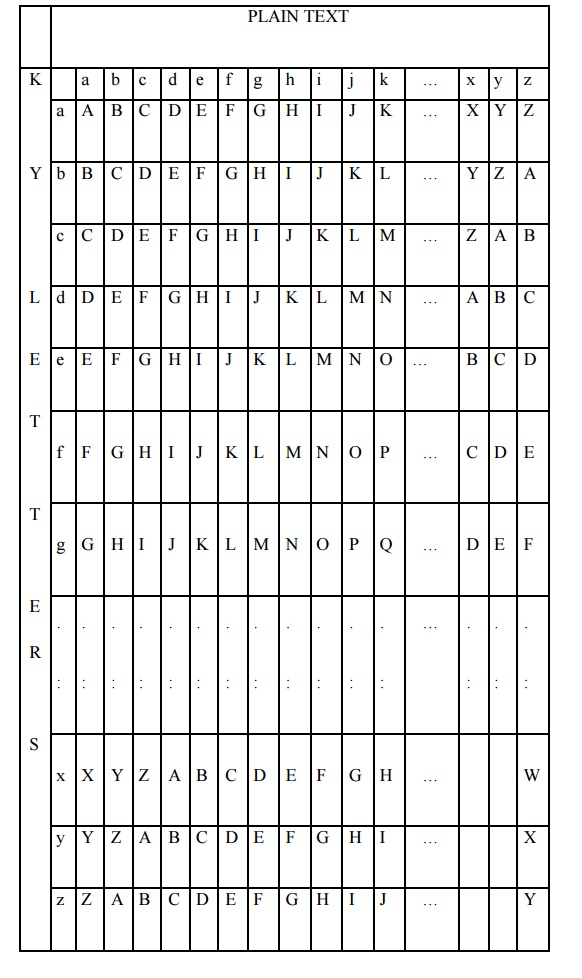
Decryption is equally simple. The key letter again identifies the row. The position of the cipher text letter in that row determines the column, and the plaintext letter is at the top of that column.
Strength of Vigenere cipher
There are multiple ciphertext letters for each plaintext letter
Letter frequency inforamiton is obscured.
One Time Pad Cipher
It is an unbreakable cryptosystem. It represents the message as a sequence of 0s and 1s. this can be accomplished by writing all numbers in binary, for example, or by using ASCII. The key is a random sequence of 0‟s and 1‟s of same length as the message.
Once a key is used, it is discarded and never used again. The system can be expressed as follows:
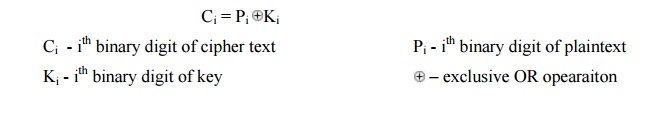
Thus the cipher text is generated by performing the bitwise XOR of the plaintext and the key. Decryption uses the same key. Because of the properties of XOR, decryption simply involves the same bitwise operation:
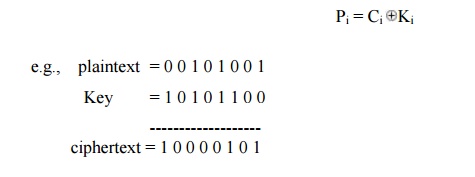
Advantage:
Encryption method is completely unbreakable for a ciphertext only attack.
Disadvantages
It requires a very long key which is expensive to produce and expensive to transmit.
Once a key is used, it is dangerous to reuse it for a second message; any knowledge on the first message would give knowledge of the second.
2 TRANSPOSITION TECHNIQUES
All the techniques examined so far involve the substitution of a cipher text symbol for a plaintext symbol. A very different kind of mapping is achieved by performing some sort of permutation on the plaintext letters. This technique is referred to as a transposition cipher.
Rail fence is simplest of such cipher, in which the plaintext is written down as a sequence of diagonals and then read off as a sequence of rows.
Plaintext = meet at the school house
To encipher this message with a rail fence of depth 2, we write the message as follows:
m e a t e c o l o s
e t t h s H o h u e
The encrypted message is
MEATECOLOSETTHSHOHUE
Row Transposition Ciphers-A more complex scheme is to write the message in a rectangle, row by row, and read the message off, column by column, but permute the order of the columns. The order of columns then becomes the key of the algorithm.
e.g., plaintext = meet at the school house

CT = ESOTCUEEHMHLAHSTOETO
A pure transposition cipher is easily recognized because it has the same letter frequencies as the original plaintext. The transposition cipher can be made significantly more secure by performing more than one stage of transposition. The result is more complex permutation that is not easily reconstructed.
LINEAR FEEDBACK SHIFT REGISTER (LFSR)
An LFSR of length m consists of m stages numbered 1, 2, . . . ,m, each storing one bit and having one input and one output; together with a clock which controls the movement of data.
The vector (k1, k2, · · · , km) would be used to initialize the shift register. During each unit of time the following operations would be performed concurrently
k1 would be tapped as the next keystream bit
k2, · · · , km would each be shifted one stage to the left
the “new” value of km would be computed to be
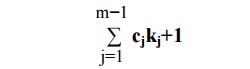
the linear feedback is carried out by tapping certain stages of the register (as specified by the constants cj having the value “1”) and computing a sum modulo 2 (which is an exclusive-or).
Applications:
· Pseudo-random number
· Pseudo-noise sequences
· Digital counters


